Mathematical definition of the Short-time Fourier Transform (STFT) is given by
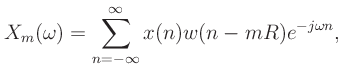
The window used in the STFT, ![]() , must satisfy the Constant
Overlap-Add (COLA) property:
, must satisfy the Constant
Overlap-Add (COLA) property:
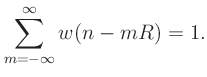
If COLA is satisfied, then the sum of successive DTFTs over time
equals the DTFT of the whole signal ![]() , that is:
, that is:
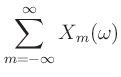 |
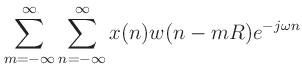 |
||
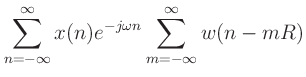 |
|||
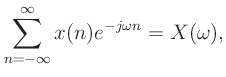 if COLA. if COLA. |
Rectangle window is COLA if there is no overlap. Bartlett window, and all the Hamming family are COLA with 50 % overlap (when end points are handled correctly).