The Feedforward Comb Filter

Increasing the delay on the second term of the ``simple lowpass filter'' can be seen as replacing that term with a delay line, yielding

$$y(n) = x(n) + gx(n-M),$$

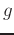where $g$ is the coefficient multiplying the delay.

Figure 14: A feedforward comb filter.

Figure 15: The comb filter magnitude response.

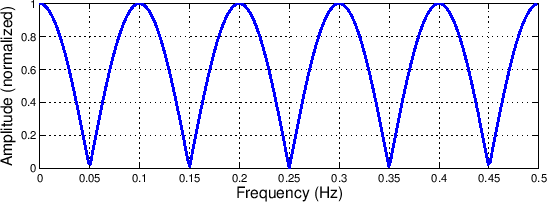The name of the filter comes from the fact that the magnitude response resembles the teeth of a comb, and because there are not feedback terms.