Linearity and Time Invariance

• A filter is linear if it satisfies the following two properties:
  1. Scaling: the amplitude of the output is proportional to the amplitude of the input (i.e., scaling can be done either at the input or the output)
     $$\mathcal{L}\{gx(\cdot)\} = g\mathcal{L}\{x(\cdot)\}$$

  2. Superposition: the output due to a sum of input signals is equal to the sum of outputs due to each signal alone.
     $$\mathcal{L}\{x_1(\cdot) + x_2(\cdot)\} = \mathcal{L}\{x_1(\cdot)\} + \mathcal{L}\{x_2(\cdot)\}$$

• A filter is time-invariant if its behaviour is not dependent on time:
  • if the input signal is delayed by 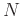$N$ samples, the output waveform is simply delayed by 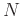$N$ samples:
    $$\mathcal{L}\{x(\cdot-N)\} = \mathcal{L}_{n-N}\{x(\cdot)\} = y(n-N)$$