Notches occur in the spectrum as a result of destructive
interference.
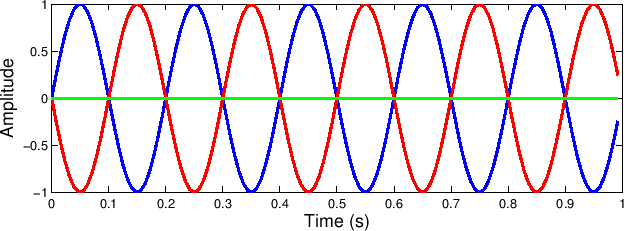
Recall that delaying a sine tone 180 degrees (1/2 a cycle) and
summing with the original will cause the signal to disappear at the
output.
Figure 17:
Complete destructive interference.
|
 |
If a sinusoid has a frequency of 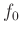 , then a delay of 1/2
cycle corresponds to a delay of
, then a delay of 1/2
cycle corresponds to a delay of
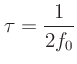
seconds
or
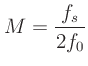
samples
``Mus 270a: Introduction to Digital Filters''
by Tamara Smyth,
Department of Music, University of California, San Diego.
Download PDF version (filters.pdf)
Download compressed PostScript version (filters.ps.gz)
Download PDF `4 up' version (filters_4up.pdf)
Download compressed PostScript `4 up' version (filters_4up.ps.gz)
Copyright © 2019-02-25 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() , then a delay of 1/2
cycle corresponds to a delay of
, then a delay of 1/2
cycle corresponds to a delay of
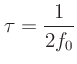 seconds
seconds
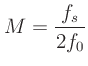 samples
samples