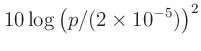Recall that intensity is proportional to sound
pressure amplitude squared:
Though 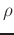 and
and 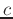 are dependent on temperature, their product is
often approximated by 400.
When
are dependent on temperature, their product is
often approximated by 400.
When
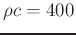 , sound pressure level
, sound pressure level 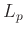 (SPL) is
equivalent to sound intensity level, and is expressed in dB by:
(SPL) is
equivalent to sound intensity level, and is expressed in dB by:
where
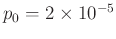 is the threshold of hearing for
amplitude of pressure variations.
is the threshold of hearing for
amplitude of pressure variations.
``Music 270a: Fundamentals of Audio, Acoustics and Sound''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (funAudio.pdf)
Download compressed PostScript version (funAudio.ps.gz)
Download PDF `4 up' version (funAudio_4up.pdf)
Download compressed PostScript `4 up' version (funAudio_4up.ps.gz)
Copyright © 2019-09-30 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>