| (1) |
The FFT, or ``fast fourier transform'' is an efficient implementation of the discrete fourer transform if the signal length is a power of two. In this example, we will use Matlab to take the FFT. Recall our simple discrete sinusoid is
| (1) |
N = 64; % signal length (power of 2) T = 1; % sampling period (and rate) is set to 1 A = 1; % sinusoid amplitude phi = 0; % phase of zero f = 0.25; % frequency (under Nyquist limit) nT = [0:N-1]*T; % discrete time axis x = cos(2*pi*f*nT + phi); % sinusoid X = fft(x);In the last line, we use Matlab's fft function to obtain the spectrum of the sinusoid. Since X is complex, we do no usually plot it as is. Rather, to obtain a more meaningful graph, we first obtain the magnitude before plotting. Recall that the magnitude of a complex number
mag 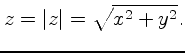 |
(2) |
magX = abs(X);to our code above we will have a sequence of real numbers representing the magnitude of the frequency components.
Likewise, we may obtain the phase using Matlab's angle function:
argX = angle(X);Alternatively, we could use the following:
angleX = atan2(imag(X), real(X));which implements the fact that the angle is given by
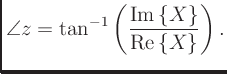
Let's now make 3 plots: one to plot the time-domain evolution, one to plot the magnitude of the fft on a linear scale, and finally one to plot the magnitude on a dB scale.
% Plot time data:
figure(1);
subplot(3,1,1);
plot(n,x,'*k');
ni = [0:.1:N-1]; % Interpolated time axis
hold on;
plot(ni,A*cos(2*pi*ni*f*T+phi),'-k'); grid off;
title('Sinusoid at 1/4 the Sampling Rate');
xlabel('Time (samples)');
ylabel('Amplitude');
text(-8,1,'a)');
hold off;
% Plot spectral magnitude:
magX = abs(X);
fn = [0:1/N:1-1/N]; % Normalized frequency axis
subplot(3,1,2);
stem(fn,magX,'ok'); grid on;
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (Linear)');
text(-.11,40,'b)');
% Same thing on a dB scale:
spec = 20*log10(magX); % Spectral magnitude in dB
spec = spec - max(spec); % Normalize to 0 db max
subplot(3,1,3);
plot(fn,spec,'--ok'); grid on;
axis([0 1 -350 50]);
xlabel('Normalized Frequency (cycles per sample))');
ylabel('Magnitude (dB)');
text(-.11,50,'c)');