Harmonic Product Spectrum (HPS)

HPS (Noll 1969) measures the maximum coincidence for harmonics for each spectral frame according to

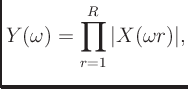$$Y(\omega) = \prod^R_{r=1} \vert X(\omega r)\vert,$$ (1)

where R is the number of harmonics being considered.

The resulting periodic correlation array $Y(\omega)$ is then searched for a maximum value of a range of possible fundamental frequencies $\omega_i$

$$\hat{Y} = \max_{\omega_i}{Y(\omega_i)}$$ (2)

to obtain the fundamental frequency estimate.

Octave errors are common (detection is sometimes an octave too high).

To correct, apply this rule: if the second peak amplitude below initially chosent pitch is approximately 1/2 of the chosen pitch AND the ratio of amplitudes is above a threshold (e.g., 0.2 for 5 harmonics), THEN select the lower octave peak as the pitch for the current frame.

Due to noise, frequencies below about 50 Hz should not be searched for a pitch.

Pros: HPS is simple to implement, does well under a wide range of conditions, and runs in real-time.

Cons: low frequency resolution must be enhanced by zero-padding, so that the spectrum can be interpolated to the nearest semitone. This means that high frequencies are also being unecessarily interpolated.

See hps.m

Figure 2: Harmonic Product Spectrum