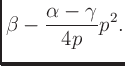The position of the peak is limited by the resolution of the
DFT/FFT and its estimation can be improved using quadratic
interpolation.
The general equation for a parabola is given by
where 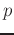 is the peak location and
is the peak location and 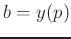 .
.
Considering the parabola at points
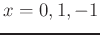 yields 3
equations,
yields 3
equations,
and 3 unknowns 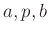 .
.
Solve for 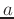 :
:
Solve for 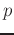 using
using 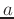 :
:
Finally, the height at peak 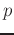 is given by
is given by
Another way (Dan Ellis)
``Music 270a: Signal Analysis''
by Tamara Smyth,
Department of Music, University of California, San Diego.
Download PDF version (analysis.pdf)
Download compressed PostScript version (analysis.ps.gz)
Download PDF `4 up' version (analysis_4up.pdf)
Download compressed PostScript `4 up' version (analysis_4up.ps.gz)
Copyright © 2019-12-02 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() yields 3
equations,
yields 3
equations,
![]() :
:
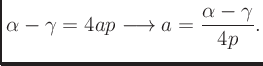
![]() using
using ![]() :
:
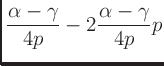
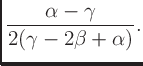
![]() is given by
is given by