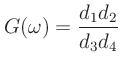Recall the amplitude response
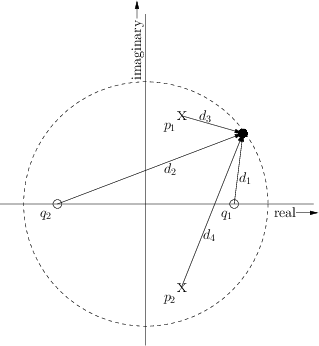
Figure 12:
Measurement of amplitude response from a pole-zero diagram
(a bi-quad section).
 |
Thus the term
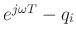 may be drawn as an arrow from the
may be drawn as an arrow from the
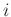 th zero to the point
th zero to the point
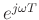 on the unit circle, and
on the unit circle, and
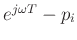 is an arrow from the
is an arrow from the 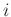 th pole.
th pole.
The amplitude response at frequency 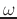 is given by
is given by
``Mus 270a: Introduction to Digital Filters''
by Tamara Smyth,
Department of Music, University of California, San Diego.
Download PDF version (filters.pdf)
Download compressed PostScript version (filters.ps.gz)
Download PDF `4 up' version (filters_4up.pdf)
Download compressed PostScript `4 up' version (filters_4up.ps.gz)
Copyright © 2019-02-25 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
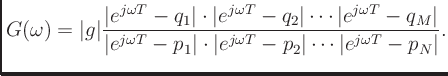
![]() may be drawn as an arrow from the
may be drawn as an arrow from the
![]() th zero to the point
th zero to the point
![]() on the unit circle, and
on the unit circle, and
![]() is an arrow from the
is an arrow from the ![]() th pole.
th pole.
![]() is given by
is given by