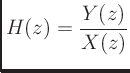Transfer Function Summary

• A transfer function provides an algebraic representation of a LTI filter in the frequency domain.

• Recall, that we can determine the frequency response by observing the effects of the filter at different frequencies, a technique called sine-wave analysis.

• The gain or amplitude response of the filter at a given frequency is determined by the ratio of the the peak output amplitude to the peak input amplitude at this frequency.

• The phase response of the of the filter at a given frequency is determined by the difference between the output and input phases at a given frequency.

• The transfer function of an LTI filter is given by
  $$H(z) = \frac{Y(z)}{X(z)}$$
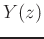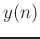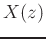  where $Y(z)$ is the z transform of the output signal $y(n)$ and $X(z)$ is the z transform of the input signal $x(n)$.

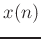• The transfer function is equal to the z transform of the impulse response.