The transfer function is the ratio of the output to the input.
Group the 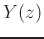 terms together on the
left hand side and factor out common terms
terms together on the
left hand side and factor out common terms 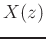 and
and 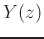 :
:
In defining the following polynomials:
the 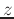 transform of the difference equation becomes
transform of the difference equation becomes
In solving for 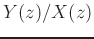 we obtain the transfer function
we obtain the transfer function
where 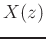 and
and 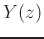 are the
are the 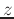 transforms of the input and output
signal, respectively.
transforms of the input and output
signal, respectively.
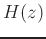 is the
is the 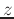 transform of the impulse
response describing the filter.
transform of the impulse
response describing the filter.
``Mus 270a: Introduction to Digital Filters''
by Tamara Smyth,
Department of Music, University of California, San Diego.
Download PDF version (filters.pdf)
Download compressed PostScript version (filters.ps.gz)
Download PDF `4 up' version (filters_4up.pdf)
Download compressed PostScript `4 up' version (filters_4up.ps.gz)
Copyright © 2019-02-25 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() terms together on the
left hand side and factor out common terms
terms together on the
left hand side and factor out common terms ![]() and
and ![]() :
:
![]() we obtain the transfer function
we obtain the transfer function
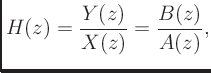
![]() is the
is the ![]() transform of the impulse
response describing the filter.
transform of the impulse
response describing the filter.