Transform Properties

Two (2) important properties of 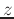transforms:

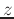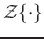The transform $\mathcal{Z}\{\cdot\}$ is a linear operator which means, by definition

$\displaystyle \mathcal{Z}\{\alpha x_1(n)+\beta x_2(n) \}$ $\displaystyle =$ $\displaystyle \alpha\mathcal{Z}\{x_1(n)\} + \beta\mathcal{Z}\{x_2(n)\}$

$\displaystyle \triangleq$ $\displaystyle \alpha X_1(z) + \beta X_2(z).$
From the shift theorem for 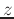transforms, the 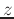transform of a signal delayed by 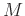samples is given by

$\displaystyle \mathcal{Z}\{x(n-M)\} = z^{-M}X(z).$

Shift Theorem:

$\fbox{\parbox{5.7in}{A \textbf{delay of $M$\ samples} in the time domain corresponds to a \textbf{multiplication by $z^{-M}$} in the frequency domain.}}$

``Mus 270a: Introduction to Digital Filters'' by Tamara Smyth, Department of Music, University of California, San Diego.

Download PDF version (filters.pdf)
Download compressed PostScript version (filters.ps.gz)
Download PDF `4 up' version (filters_4up.pdf)
Download compressed PostScript `4 up' version (filters_4up.ps.gz)

$\displaystyle \mathcal{Z}\{\alpha x_1(n)+\beta x_2(n) \}$	$\displaystyle =$	$\displaystyle \alpha\mathcal{Z}\{x_1(n)\} + \beta\mathcal{Z}\{x_2(n)\}$
	$\displaystyle \triangleq$	$\displaystyle \alpha X_1(z) + \beta X_2(z).$