Transform of the Difference Equation

Given the general difference equation for LTI filters,

$\displaystyle y(n) = b_0x(n)$	$\displaystyle +$	$\displaystyle b_1x(n-1) + \cdots + b_Mx(n-m)$
	$\displaystyle -$	$\displaystyle a_1y(n-1) - \cdots - a_Ny(n-N),$

taking the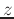

transform of both sides yields

$\displaystyle \mathcal{Z}\{y(\cdot)\}$	$\displaystyle =$	$\displaystyle \mathcal{Z}\{b_0x(n) + b_1x(n-1) + \cdots + b_Mx(n-m)$
		$\displaystyle \qquad\qquad - a_1y(n-1) - \cdots - a_Ny(n-N)\}.$

Apply the linearity property to obtain

$\displaystyle \mathcal{Z}\{y(\cdot)\}$	$\displaystyle =$	$\displaystyle b_0\mathcal{Z}\{x(n)\} + b_1\mathcal{Z}\{x(n-1)\}$
		$\displaystyle + \cdots + b_M\mathcal{Z}\{x(n-M)\}$
		$\displaystyle -a_1\mathcal{Z}\{y(n-1)\}-\cdots- a_N\mathcal{Z}\{x(n-N)\},$

and the shift theorem to obtain

$\displaystyle Y(z)$	$\displaystyle =$	$\displaystyle b_0X(z)+ b_1z^{-1}X(z)+ \cdots + b_Mz^{-M}X(z)$
		$\displaystyle \qquad\qquad-a_1z^{-1}Y(z)-\cdots-a_Nz^{-N}Y(z).$

``Mus 270a: Introduction to Digital Filters'' by Tamara Smyth, Department of Music, University of California, San Diego.