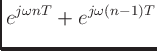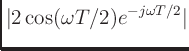On each pass through the delay-line loop, a partial at frequency 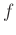 is subject to an attenuation equal to the loop amplitude response
is subject to an attenuation equal to the loop amplitude response
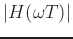 .
.
The frequency response
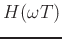 of the simple lowpass filter
may be found by testing with a complex sinusoid
of the simple lowpass filter
may be found by testing with a complex sinusoid
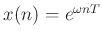 :
:
where
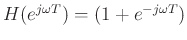 .
.
The gain of the filter is given by
``Music 206: Introduction to Delay and Filters II''
by Tamara Smyth,
Computing Science, Simon Fraser University.
Download PDF version (filtersDelayII.pdf)
Download compressed PostScript version (filtersDelayII.ps.gz)
Download PDF `4 up' version (filtersDelayII_4up.pdf)
Download compressed PostScript `4 up' version (filtersDelayII_4up.ps.gz)
Copyright © 2019-04-18 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() is subject to an attenuation equal to the loop amplitude response
is subject to an attenuation equal to the loop amplitude response
![]() .
.
![]() of the simple lowpass filter
may be found by testing with a complex sinusoid
of the simple lowpass filter
may be found by testing with a complex sinusoid
![]() :
: