- A waveshaper with a linear transfer function will not produce
distortion, but any deviation from a line will introduce some sort of
distortion and change the spectrum of the input.
- To control the maximum harmonic in the spectrum (say, for the
purpose of avoiding aliasing), a transfer function is expressed as a
polynomial:
where the order of the polynomial is 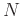 , and
, and 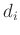 are the polynomial
coefficients.
are the polynomial
coefficients.
- When driven with a
sinusoid, a waveshaper with a transfer function of order
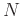 produces
no harmonics above the
produces
no harmonics above the 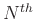 harmonic.
harmonic.
- When the driving sinusoid is of unit amplitude, the amplitudes
of the various harmonics can be calculated using the right side of
Pascal's triangle.
``Music 270a: Waveshaping Synthesis''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (waveshaping.pdf)
Download compressed PostScript version (waveshaping.ps.gz)
Download PDF `4 up' version (waveshaping_4up.pdf)
Download compressed PostScript `4 up' version (waveshaping_4up.ps.gz)
Copyright © 2019-03-03 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>