If the input cosine has an amplitude of 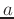 , then the output in
polynomial form becomes
, then the output in
polynomial form becomes
Example: Given the waveshapping transfer function
an input sinusoid with amplitude 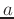 yields the output
yields the output
with the amplitude of each harmonic calculated using Pascal's
triangle to obtain
Because an increase in 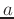 (typically between 0
and 1) produces a richer output spectrum, it is often referred to as a
distortion index (analogous to the index of modulation in FM
synthsis).
(typically between 0
and 1) produces a richer output spectrum, it is often referred to as a
distortion index (analogous to the index of modulation in FM
synthsis).
``Music 270a: Waveshaping Synthesis''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (waveshaping.pdf)
Download compressed PostScript version (waveshaping.ps.gz)
Download PDF `4 up' version (waveshaping_4up.pdf)
Download compressed PostScript `4 up' version (waveshaping_4up.ps.gz)
Copyright © 2019-03-03 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() , then the output in
polynomial form becomes
, then the output in
polynomial form becomes
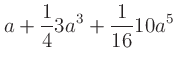
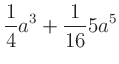
![]() (typically between 0
and 1) produces a richer output spectrum, it is often referred to as a
distortion index (analogous to the index of modulation in FM
synthsis).
(typically between 0
and 1) produces a richer output spectrum, it is often referred to as a
distortion index (analogous to the index of modulation in FM
synthsis).