More generally, linear interpolation is given by
where 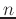 is the integer part of the original
index value, and
is the integer part of the original
index value, and 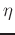 is the fractional part, indicating
how far from
is the fractional part, indicating
how far from 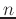 we want to interpolate,
we want to interpolate,
Below is a Matlab function which implements linear interpolation.
function y = lininterp(w, x);
% LININTERP Linear interpolation.
% Y = LININTERP(W, X) where Y is the output,
% X is the input indeces, not necessarily
% integers, and W is the transfer function
% indexed by X.
n = floor(x);
eta = x-n;
w = [w 0];
y = (1-eta).*w(n) + eta.*w(n+1);
y = y(1:length(x));
``Music 270a: Waveshaping Synthesis''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (waveshaping.pdf)
Download compressed PostScript version (waveshaping.ps.gz)
Download PDF `4 up' version (waveshaping_4up.pdf)
Download compressed PostScript `4 up' version (waveshaping_4up.ps.gz)
Copyright © 2019-03-03 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>