Rather than rounding or truncating index values,
it is more accurate to interpolate
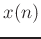 .
.
Linear interpolation of 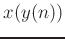 :
:
- consider a line between neighboring values of
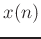 indexed at
the floor and ceiling of
indexed at
the floor and ceiling of 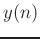 :
:
- a value that would lie on the line is
inferred depending on the fractional part of the index.
Example: if 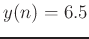 , the inferred value would
be on the line between
, the inferred value would
be on the line between 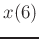 and
and 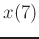 , equidistant from
indeces 6 and 7:
, equidistant from
indeces 6 and 7:
More generally, for
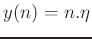 ,
where
,
where 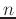 is the integer part and
is the integer part and 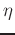 is the fractional part,
is the fractional part,
``Music 171: Wavetables and Samplers''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (wavetables.pdf)
Download compressed PostScript version (wavetables.ps.gz)
Download PDF `4 up' version (wavetables_4up.pdf)
Download compressed PostScript `4 up' version (wavetables_4up.ps.gz)
Copyright © 2019-10-15 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() .
.
![]() :
:
![]() , the inferred value would
be on the line between
, the inferred value would
be on the line between ![]() and
and ![]() , equidistant from
indeces 6 and 7:
, equidistant from
indeces 6 and 7:
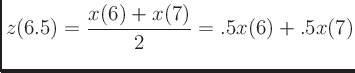
![]() ,
where
,
where ![]() is the integer part and
is the integer part and ![]() is the fractional part,
is the fractional part,
![]()