The difference (instead of the sum) of adjacent
samples:
is like changing the coefficient of 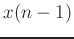 to -1.
to -1.
At 0 Hz:
At 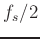 Hz:
Hz:
``Music 171: Introduction to Delay and Filters''
by Tamara Smyth,
Computing Science, Simon Fraser University.
Download PDF version (filt171.pdf)
Download compressed PostScript version (filt171.ps.gz)
Download PDF `4 up' version (filt171_4up.pdf)
Download compressed PostScript `4 up' version (filt171_4up.ps.gz)
Copyright © 2019-11-21 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() Hz:
Hz: