The impulse response 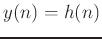 is equivalent to coefficients of our
FIR filter
is equivalent to coefficients of our
FIR filter 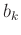 .
.
This can be shown using the general FIR equation, with input
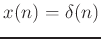 (recall
(recall 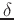 only has a nonzero value when
only has a nonzero value when  ).
).
When the relation between the input 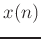 and the output
and the output 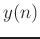 of the FIR filter is expressed in terms of the input and impulse
response, we say the output is obtained by convolving the
sequences
of the FIR filter is expressed in terms of the input and impulse
response, we say the output is obtained by convolving the
sequences 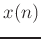 and
and 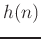 .
.
``Music 206: Delay and Digital Filters I''
by Tamara Smyth,
Computing Science, Simon Fraser University.
Download PDF version (filtersDelayI.pdf)
Download compressed PostScript version (filtersDelayI.ps.gz)
Download PDF `4 up' version (filtersDelayI_4up.pdf)
Download compressed PostScript `4 up' version (filtersDelayI_4up.ps.gz)
Copyright © 2020-01-14 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() is equivalent to coefficients of our
FIR filter
is equivalent to coefficients of our
FIR filter ![]() .
.
![]() (recall
(recall ![]() only has a nonzero value when
only has a nonzero value when ![]() ).
).
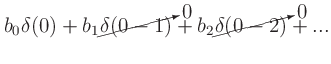
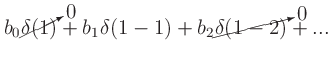
![]() and the output
and the output ![]() of the FIR filter is expressed in terms of the input and impulse
response, we say the output is obtained by convolving the
sequences
of the FIR filter is expressed in terms of the input and impulse
response, we say the output is obtained by convolving the
sequences ![]() and
and ![]() .
.