Intuitive Analyis at High Frequencies

The running average of an input signal with significant variation from sample to sample will be very different from its input.

At 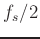(Nyquist limit)

$\displaystyle x_2(n) = [A, -A, A, ...].$

The output of the filter is

$\displaystyle y(n)$	$\displaystyle =$	$\displaystyle x_2(n) + x_2(n-1)$
	$\displaystyle =$	$\displaystyle \quad [A, -A, A, ....]$
$\displaystyle$		$\displaystyle +$ $\displaystyle [0, A, -A, A, ...]$
	$\displaystyle =$	$\displaystyle \quad [A, 0, 0, 0, ...]$

$\fbox{\parbox{5.5in}{The output is different from the input-complete attenuation.}}$

``Music 206: Delay and Digital Filters I'' by Tamara Smyth, Computing Science, Simon Fraser University.