It is possible to determine the exact amplitude of the sidebands using the help of bessel functions.
We can also make use of a rule of thumb for how to set
the modulation index ![]() to obtain a frequency deviation
to obtain a frequency deviation ![]() about the
the carrier frequency:
about the
the carrier frequency:
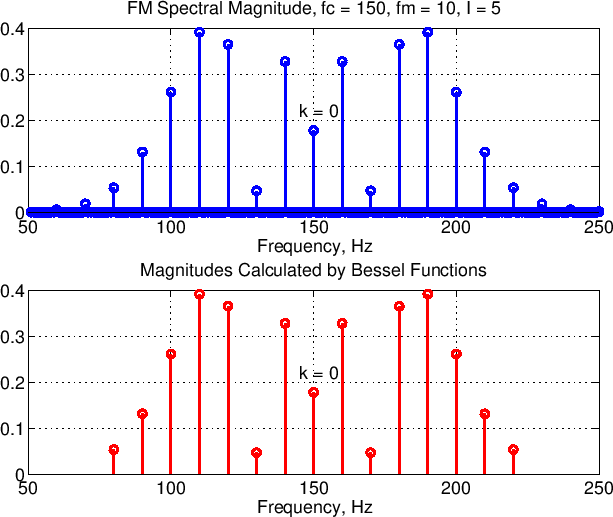
When ![]() , the index
, the index ![]() is also zero, and no modulation
occurs. Increasing
is also zero, and no modulation
occurs. Increasing ![]() causes the sidebands to acquire more power at
the expense of the power in the carrier frequency.
causes the sidebands to acquire more power at
the expense of the power in the carrier frequency.
The deviation ![]() acts as a control on FM bandwidth.
acts as a control on FM bandwidth.
The actual amplitude of each sideband can be determined by bessel functions.