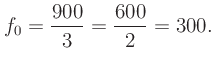In determining the fundamental frequency of an FM sound,
first represent the ratio of the carrier and modulator frequencies as a
reduced fraction,
where 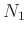 and
and 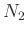 are integers with no common factors.
are integers with no common factors.
The fundamental frequency is then given by
Example: a carrier frequency 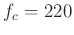 and modulator frequency
and modulator frequency
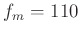 yields the ratio of
yields the ratio of
and a fundamental frequency of
Likewise the ratio of 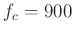 to
to 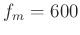 is 3:2 and the
fundamental frequency is given by
is 3:2 and the
fundamental frequency is given by
``Music 270a: Modulation''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (modulation.pdf)
Download compressed PostScript version (modulation.ps.gz)
Download PDF `4 up' version (modulation_4up.pdf)
Download compressed PostScript `4 up' version (modulation_4up.ps.gz)
Copyright © 2019-10-28 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
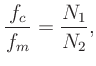
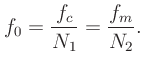
![]() and modulator frequency
and modulator frequency
![]() yields the ratio of
yields the ratio of
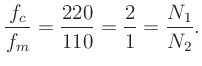
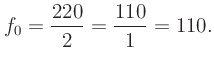
![]() to
to ![]() is 3:2 and the
fundamental frequency is given by
is 3:2 and the
fundamental frequency is given by