Multiplication of Sinusoids

What happens when we multiply a low frequency sinusoids with a higher frequency sinusoid (or any two sinusoids)?

$$\sin(2\pi(220)t)\cos(2\pi(2)t)$$

$$= \left(\frac{e^{j2\pi (220)t}-e^{-j2\pi (220)t}}{2j}\right) \left(\frac{e^{j2\pi (2)t}+e^{-j2\pi (2)t}}{2}\right)$$

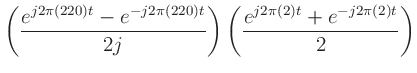$$= \frac{1}{4j}\left[e^{j2\pi (222)t} - e^{-j2\pi (222)t} + e^{j2\pi (218)t} - e^{-j2\pi (218)t}\right]$$

$$= \frac{1}{2}\left[\sin(2\pi(222)t)+\sin(2\pi(218)t)\right]$$

The product of two real sinusoids results in the sum of two real sinusoids (having different frequencies).

Interestingly, the resulting spectral components (those in the sum) are not at the frequencies in the product. Rather, they are at their sum and the difference.

Sinusoidal multiplication can therefore be expressed as an addition.