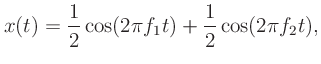Ring modulation (RM), introduced as the beat note waveform,
occurs when modulation is applied directly to the amplitude input of
the carrier modulator:
Recall that this multiplication can also be expressed as the sum
of sinusoids using the inverse of Euler's formula:
where
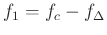 and
and
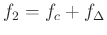 .
.
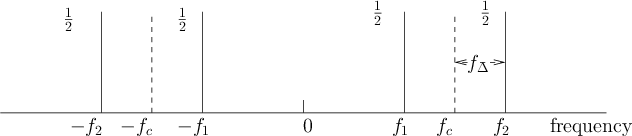
Figure 2:
Spectrum of ring modulation.
 |
``Music 270a: Modulation''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (modulation.pdf)
Download compressed PostScript version (modulation.ps.gz)
Download PDF `4 up' version (modulation_4up.pdf)
Download compressed PostScript `4 up' version (modulation_4up.ps.gz)
Copyright © 2019-10-28 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>