Additional Modes

When modes are independent, the system can vibrate in one mode with minimal excitation of another.

Unless constrained to one-dimension, the masses can also move transversely (at right-angles to the springs).

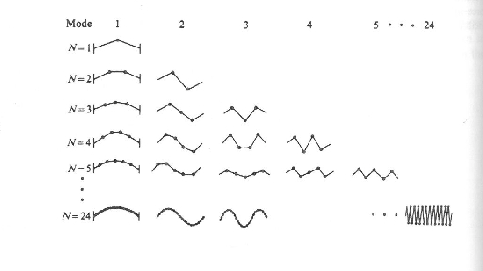
An additional mass adds an additional mode of vibration.

An N-mass system has N modes per degree of freedom.

As N gets very large, it becomes convenient to view the system as a continuous string with a uniform mass density and tension.

**Figure 8:** Increasing the number of masses (Science of Sound).
$\scalebox{.55}{\includegraphics{eps/multiple-mass-spring.eps}}$

``MUS 206: Mechanical Vibration'' by Tamara Smyth, Department of Music, University of California, San Diego (UCSD).