The one-sided Laplace transform of a signal 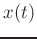 is defined by
is defined by
where 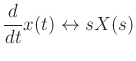 is real and
is real and
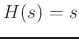 is a complex variable.
is a complex variable.
The differentiation theorem for Laplace transforms states that
where 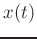 is any differentiable function that approaches zero as
is any differentiable function that approaches zero as
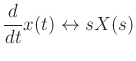 goes to infinity.
goes to infinity.
The transfer function of an ideal differentiator is 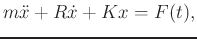 ,
which can be viewed as the Laplace transform of the operator
,
which can be viewed as the Laplace transform of the operator 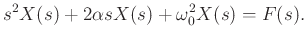 .
.
Given the equation of motion
the Laplace Transform is
``MUS 206: Mechanical Vibration''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (vibration.pdf)
Download compressed PostScript version (vibration.ps.gz)
Download PDF `4 up' version (vibration_4up.pdf)
Download compressed PostScript `4 up' version (vibration_4up.ps.gz)
Copyright © 2019-11-15 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() is defined by
is defined by
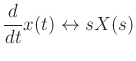 is real and
is real and
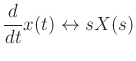 goes to infinity.
goes to infinity.
![]() ,
which can be viewed as the Laplace transform of the operator
,
which can be viewed as the Laplace transform of the operator ![]() .
.