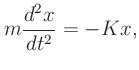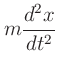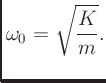The solution to
is a function proportional to its second derivative.
This condition is met by the sinusoid:
Substituting into the equation of motion yields:
showing that the natural frequency of vibration is
``MUS 206: Mechanical Vibration''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (vibration.pdf)
Download compressed PostScript version (vibration.ps.gz)
Download PDF `4 up' version (vibration_4up.pdf)
Download compressed PostScript `4 up' version (vibration_4up.ps.gz)
Copyright © 2019-11-15 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>