- The transfer function for the first-order shelf filter is given by
- The coefficients are given by
where
and
- To form the coefficients of a prototype shelf filter with a transition
frequency of
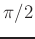
- The parameter
is the coefficient of the first-order allpass transformation warping
the prototype filter to the proper transition frequency.
- An efficient way to model the frequency response is to use a cascade
of minimum-phase first-order shelf filters
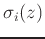 ,
,
- Unlike with other methods, the shelf filter coefficients are easily
computed in real time.
- Since the shelf filters are first order, they have real poles
and zeros, and are relatively free of artifacts when made time
varying.
- In designing the prototype filters for different orders
it was discovered that a cascade of shelf filters with
band-edge gains (in units of amplitude) and transition frequencies
(in
radians
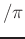 )
given by
)
given by
has a transfer function which is an excellent approximation to
 for a wide range of filter orders
for a wide range of filter orders 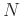 , tube lengths
, tube lengths
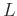 , tube radii
, tube radii 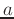 , and sampling rates
, and sampling rates 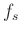 .
.
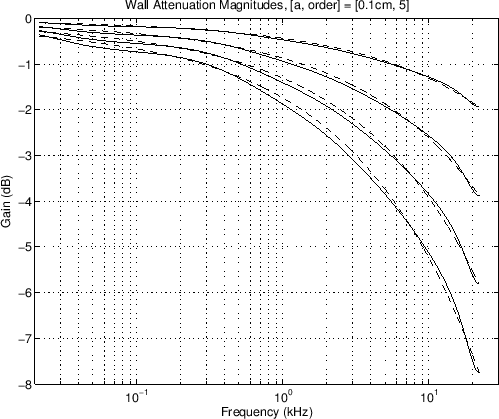
Figure 19:
Computed and shelf filter cascade wall
loss filter magnitude at various tube radii: 0.1 (lower) - 0.5 (upper) cm.
|
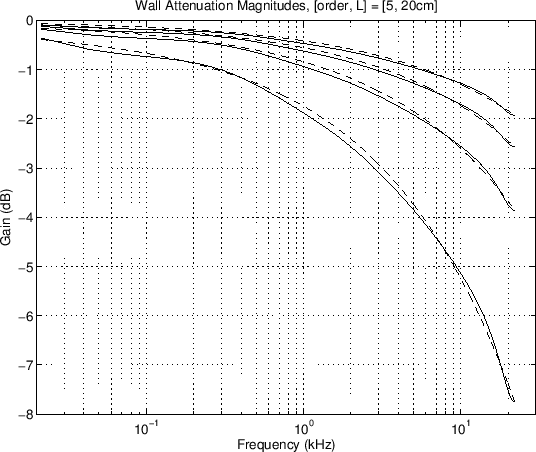 |
Figure 20:
Computed and shelf filter cascade wall
loss filter magnitude at various tube lengths: 5 (upper) - 25 (lower) cm.
|
 |
``MUS 206: Modeling Acoustic Tubes and Wind Instrument Bores/Bells''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (wind.pdf)
Download compressed PostScript version (wind.ps.gz)
Download PDF `4 up' version (wind_4up.pdf)
Download compressed PostScript `4 up' version (wind_4up.ps.gz)
Copyright © 2019-05-22 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
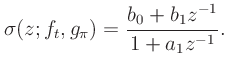
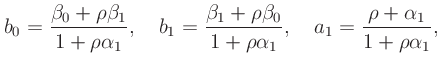
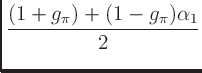
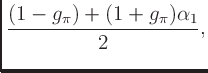
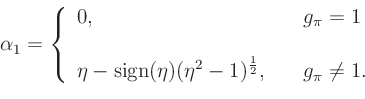
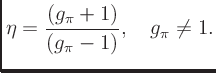
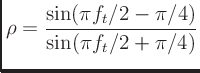
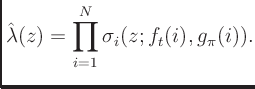
![$\displaystyle \exp\left\{
\frac{[(i-\frac{1}{2})/N]^{\frac{1}{2}}}{\sum_{k=1}^N...
...\frac{1}{2})/N]^{\frac{1}{2}}} \cdot \ln \vert\lambda(2\pi f_s/2)\vert\right\},$](img157.png)
![$\displaystyle [(i-\frac{1}{2}) / N]^3,$](img159.png)

