The complex exponential signal (or complex sinusoid) is
defined as
It may be expressed in Cartesian form using Euler's formula:
As with the real sinusoid,
- A is the amplitude given by
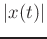
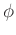 is the initial phase
is the initial phase
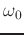 is the frequency in rad/sec
is the frequency in rad/sec
-
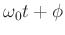 is the instantaneous phase, also denoted
is the instantaneous phase, also denoted 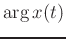 .
.
``Music 270a: Complex Exponentials and Spectrum Representation''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (compExpAndSpecRep.pdf)
Download compressed PostScript version (compExpAndSpecRep.ps.gz)
Download PDF `4 up' version (compExpAndSpecRep_4up.pdf)
Download compressed PostScript `4 up' version (compExpAndSpecRep_4up.ps.gz)
Copyright © 2019-10-21 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
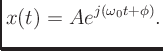
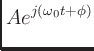
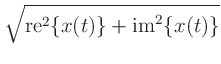
![$\displaystyle \sqrt{A^2[\cos^2(\omega t+\phi) + \sin^2(\omega t+\phi)]}$](img50.png)