Euler's Formula

From the result of sinusoidal projection, we can see how Euler's famous formula for the complex exponential was obtained:

$$e^{j\theta} = \cos\theta + j\sin\theta,$$

valid for any point ( 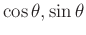$\cos\theta, \sin\theta$) on a circle of radius one (1).

Euler's formula can be further generalized to be valid for any complex number 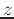$z$:

$$z = re^{j\theta} = r\cos\theta + jr\sin\theta.$$

Though called ``complex'', these number usually simplify calculations considerably--particularly in the case of multiplication and division.