Notch and Bandpass Filters

Consider next, changing the delay value of the second term:

$$y(n) = x(n) + x(n-2).$$

This changes the filter order to 2 and effectively sets the 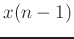$x(n-1)$ term to zero.

This filter passes both DC and the Nyquist limit, but attenuates 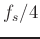$f_s/4$. It is a notch filter.

The filter given by

$$y(n) = x(n) - x(n-2)$$

rejects DC and the Nyquist limit, and boosts 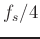$f_s/4$. It is a bandpass filter.