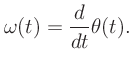A chirp signal is one that sweeps linearly from a low
to a high frequency.
To produce a chirping sinusoid, modifying its equation so the
frequency is time-varying will likely produce better results than
concatenating segments.
Recall that the original equation for a sinusoid is given by
where the instantaneous phase, given by
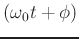 , changes
linearly with time.
, changes
linearly with time.
Notice that the time derivative of the phase is the radian
frequency of the sinusoid 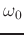 , which in this case is a
constant.
, which in this case is a
constant.
More generally, if
the instantaneous frequency is given by
``Music 270a: Modulation''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (modulation.pdf)
Download compressed PostScript version (modulation.ps.gz)
Download PDF `4 up' version (modulation_4up.pdf)
Download compressed PostScript `4 up' version (modulation_4up.ps.gz)
Copyright © 2019-10-28 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() , which in this case is a
constant.
, which in this case is a
constant.