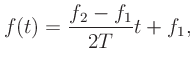Now, let's make the phase quadratic, and thus non-linear
with respect to time.
The instantaneous frequency (the derivative
of the phase 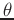 ), becomes
), becomes
which in Hz becomes
Notice the frequency is no longer constant but changing linearly in time.
To create a sinusoid with frequency sweeping linearly from 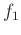 to
to 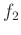 , consider the equation for a line
, consider the equation for a line
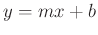 to obtain
to obtain
where 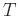 is the duration of the sweep.
is the duration of the sweep.
``Music 270a: Modulation''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (modulation.pdf)
Download compressed PostScript version (modulation.ps.gz)
Download PDF `4 up' version (modulation_4up.pdf)
Download compressed PostScript `4 up' version (modulation_4up.ps.gz)
Copyright © 2019-10-28 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() ), becomes
), becomes
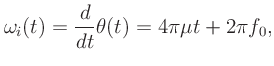
![]() to
to ![]() , consider the equation for a line
, consider the equation for a line
![]() to obtain
to obtain