Without going any further in solving this equation, it is possible to
get a sense of the effect of the modulation index ![]() from
from
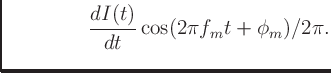 |
We may see that if ![]() is a constant (and it's derivative is zero),
the third term goes away and the instantaneous frequency becomes
is a constant (and it's derivative is zero),
the third term goes away and the instantaneous frequency becomes
Notice now that in the second term, the quantity ![]() multiplies a sinusoidal variation of frequency
multiplies a sinusoidal variation of frequency ![]() , indicating that
, indicating that
![]() determines the maximum amount by which the instantaneous
frequency deviates from the carrier frequency
determines the maximum amount by which the instantaneous
frequency deviates from the carrier frequency ![]() .
.
Since the modulating frequency ![]() is at audio rates, this
translates to addition of harmonic content.
is at audio rates, this
translates to addition of harmonic content.
Since ![]() is a function of time, the harmonic content, and
thus the timbre, of the synthesized sound may vary with time.
is a function of time, the harmonic content, and
thus the timbre, of the synthesized sound may vary with time.