A spectrum containing several harmonics can be matched by
combining the appropriate Chebyshev polynomial for each harmonic into a
single transfer function.
Let 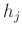 be the amplitude of the
be the amplitude of the
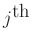 harmonic, and
harmonic, and
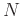 be the highest harmonic in the spectrum. The transfer function is
then given by:
be the highest harmonic in the spectrum. The transfer function is
then given by:
``Music 270a: Waveshaping Synthesis''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (waveshaping.pdf)
Download compressed PostScript version (waveshaping.ps.gz)
Download PDF `4 up' version (waveshaping_4up.pdf)
Download compressed PostScript `4 up' version (waveshaping_4up.ps.gz)
Copyright © 2019-03-03 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
![]() be the amplitude of the
be the amplitude of the
![]() harmonic, and
harmonic, and
![]() be the highest harmonic in the spectrum. The transfer function is
then given by:
be the highest harmonic in the spectrum. The transfer function is
then given by: