The finite difference approximation (FDA) amounts to replacing
derivatives by finite differences, or
The z transform of the first-order difference operator is
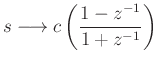 . Thus, in the frequency domain, the finite-difference
approximation may be performed by making the substitution
. Thus, in the frequency domain, the finite-difference
approximation may be performed by making the substitution
The first-order difference is first-order error accurate in 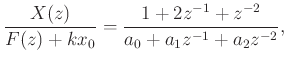 .
Better performance can be obtained using the bilinear transform, defined
by the substitution
.
Better performance can be obtained using the bilinear transform, defined
by the substitution
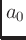
where
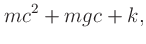
``MUS 206: Modeling Acoustic Tubes and Wind Instrument Bores/Bells''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (wind.pdf)
Download compressed PostScript version (wind.ps.gz)
Download PDF `4 up' version (wind_4up.pdf)
Download compressed PostScript `4 up' version (wind_4up.ps.gz)
Copyright © 2019-05-22 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
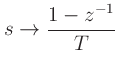
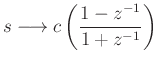 . Thus, in the frequency domain, the finite-difference
approximation may be performed by making the substitution
. Thus, in the frequency domain, the finite-difference
approximation may be performed by making the substitution
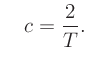
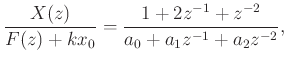 .
Better performance can be obtained using the bilinear transform, defined
by the substitution
.
Better performance can be obtained using the bilinear transform, defined
by the substitution