Using the Bilinear Transform, the transfer function becomes
where
The corresponding difference equation is
where
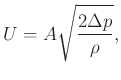 .
.
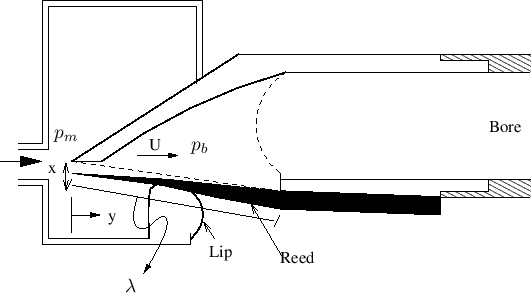
``MUS 206: Modeling Acoustic Tubes and Wind Instrument Bores/Bells''
by Tamara Smyth,
Department of Music, University of California, San Diego (UCSD).
Download PDF version (wind.pdf)
Download compressed PostScript version (wind.ps.gz)
Download PDF `4 up' version (wind_4up.pdf)
Download compressed PostScript `4 up' version (wind_4up.ps.gz)
Copyright © 2019-05-22 by Tamara Smyth.
Please email errata, comments, and suggestions to Tamara Smyth<trsmyth@ucsd.edu>
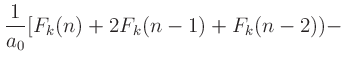
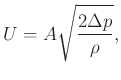 .
.